最後更新日期: 14/12/2024
Table of Contents:
📄
🚨Why It Matters
- 結構為樹形:能將資料以層級關係來儲存
- 實際例子:二元搜尋樹(Binary Search Tree)和堆積(Heap)
- 優化演算法:像是堆排序(Heap Sort)就使用樹狀資料結構
🗺️The Big Picture
💡Learned
遍歷樹的三種順序
- 前序(preorder):中 → 左 → 右
- 中序(inorder):左 → 中 → 右
- 後序(postorder):左 → 右 → 中
Coding Templates
遍歷二元樹
- DFS(遞迴)
def dfs(root):
if not root:
return
ans = 0
# do logic
dfs(root.left)
dfs(root.right)
return ans
- DFS(疊代)
def dfs(root):
stack = [root]
ans = 0
while stack:
node = stack.pop()
# do logic
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
return ans
- BFS
from collections import deque
def fn(root):
queue = deque([root])
ans = 0
while queue:
current_length = len(queue)
# do logic for current level
for _ in range(current_length):
node = queue.popleft()
# do logic
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return ans
😎94. Binary Tree Inorder Traversal
Description
給予一棵二元樹節點root,請回傳此樹的中序(Inorder)遍歷。
Example 1:

Input: root = [1,null,2,3] Output: [1,3,2]
Solutions
⭐Approach 1: Recursive Approach
中序遍歷的順序是優先讀取左子節點、根節點、右子節點,用遞迴實作一目了然。
這樣的時間與空間複雜度皆為O(N),N為節點數。
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
def helper(node):
if node:
helper(node.left)
res.append(node.val)
helper(node.right)
helper(root)
return res
😐98. Validate Binary Search Tree
Description
給予一個二元樹根節點root,請判斷此樹是否為有效二元搜尋樹(BST)。其任意節點N的特徵:
- 每個節點值皆
- 左子樹節點值皆
<N;右子樹節點值皆>N - 左右子樹皆為BST
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
Example 1:

Input: root = [2,1,3] Output: true
Example 2:

Input: root = [5,1,4,null,null,3,6] Output: false Explanation: The root node's value is 5 but its right child's value is 4.
Solutions
⭐Approach #1: Recursive Traversal with Valid Range
我們定義函式valid,由上往下地判斷節點。
這樣的時間與空間複雜度皆為O(N)。
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
def valid(node, left, right):
if not node:
return True
if not left < node.val < right:
return False
return valid(node.left, left, node.val) and valid(node.right, node.val, right)
return valid(root, float("-inf"), float("inf"))
😎100. Same Tree
Description
給予兩棵二元樹p和q的根結點,請判斷兩樹是否相同(結構和節點值)。
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
Example 1:

Input: p = [1,2,3], q = [1,2,3] Output: true
Example 2:

Input: p = [1,2], q = [1,null,2] Output: false
Example 3:

Input: p = [1,2,1], q = [1,1,2] Output: false
Solutions
我們同時遍歷兩棵樹,確認架構和節點值是否皆相同。
⭐Approach #1: Recursion
我們使用遞迴處理,同時判斷兩樹節點是否存在以及是否同值。
這樣的時間與空間複雜度皆為O(N)。
class Solution:
def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
if not p and not q:
return True
if p and q and p.val == q.val:
return self.isSameTree(p.left, q.left) and \
self.isSameTree(p.right, q.right)
else:
return False
⭐Approach #2: Iteration
我們用迭代處理:
- 定義節點判斷函式
check - 用一個佇列
deq去逐層判斷
這樣的時間與空間複雜度皆為O(N)。
from collections import deque
class Solution:
def isSameTree(self, p, q):
def check(p, q):
if not p and not q:
return True
if not q or not p:
return False
if p.val != q.val:
return False
return True
deq = deque([(p, q), ])
while deq:
p, q = deq.popleft()
if not check(p, q):
return False
if p:
deq.append((p.left, q.left))
deq.append((p.right, q.right))
return True
😎100. Same Tree101. Symmetric Tree
Description
給予一棵二元樹的根節點root,請確認此樹的結構與值是否對稱(symmetric )。
Example 1:
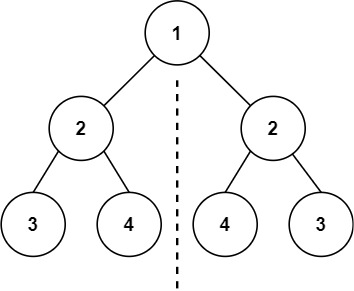
Input: root = [1,2,2,3,4,4,3] Output: true
Example 2:

Input: root = [1,2,2,null,3,null,3] Output: false
Solutions
😐102. Binary Tree Level Order Traversal
Description
給予一個二元樹根結點root,請回傳以Level order(從左到右,層層往下)所遍歷過的節點值。
Example 1:

Input: root = [3,9,20,null,null,15,7] Output: [[3],[9,20],[15,7]]
Example 2:
Input: root = [1] Output: [[1]]
Example 3:
Input: root = [] Output: []
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
Solutions
⭐Approach #1: Recursion
對於逐層地遍歷節點,我們可以用遞迴來實作:
- 使用陣列
levels存放以層為單位所遍歷過的節點 - 定義
helper:- 若
len(levels) == level:建立一個空陣列,準備存放該層節點 - 將該層節點存入陣列中
- 若節點有左右子節點,就遞迴呼叫
helper來延伸下去
- 若
- 所有
helper執行完後,levels即為所求
這樣的時間與空間複雜度皆為O(N)。
class Solution:
def levelOrder(self, root):
levels = []
if not root:
return levels
def helper(node, level):
if len(levels) == level:
levels.append([])
levels[level].append(node.val)
if node.left:
helper(node.left, level + 1)
if node.right:
helper(node.right, level + 1)
helper(root, 0)
return levels
⭐Approach #2: Iteration
我們也能用一個佇列q來實作疊代:
- 使用陣列
res來回傳達案 - 每個回合,將每層節點加到
q中 - 當
q內仍有節點時:- 初始化儲存該層節點的陣列
val - 持續將該層節點存到
val中 - 若節點有子節點,則將其加到
q中,讓下次迴圈中去處理 - 將
val加到res中
- 初始化儲存該層節點的陣列
q內沒元素時,res即為所求
這樣的時間與空間複雜度皆為O(N)。
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
res = []
q = collections.deque()
if root:
q.append(root)
while q:
val = []
for i in range(len(q)):
node = q.popleft()
val.append(node.val)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
res.append(val)
return res
😎104. Maximum Depth of Binary Tree
Description
給予一棵二元樹的根節點root,請回傳其最大深度(root到某子節點的最大節點數)。
Example 1:

Input: root = [3,9,20,null,null,15,7] Output: 3
Example 2:
Input: root = [1,null,2] Output: 2
Solutions
要找到二元樹的最大深度,我們得遍歷完整棵樹。
⭐Approach #1: Recursion
此遍歷法等同DFS:我們持續呼叫自身函式,累計高度並保留最大值。
這樣的時間複雜度為O(N),空間複雜度最糟情況也為O(N)(若樹退化成鏈結串列),樹平衡時則為O(logN),N為節點數。
class Solution:
def maxDepth(self, root):
if root is None:
return 0
else:
left_height = self.maxDepth(root.left)
right_height = self.maxDepth(root.right)
return max(left_height, right_height) + 1
⭐Approach #2: Iteration (BFS)
若用遞迴做法,我們則使用佇列q來逐層遍歷樹。
這樣的時間複雜度為O(N),空間複雜度最糟情況也為O(N)(樹退化成鏈結串列),樹平衡時則為O(logN),N為節點數。
class Solution:
def maxDepth(self, root: TreeNode) -> int:
q = deque()
if root:
q.append(root)
level = 0
while q:
for i in range(len(q)):
node = q.popleft()
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
level += 1
return level
😐105. Construct Binary Tree from Preorder and Inorder Traversal
Description
給予兩個整數陣列preorder和inorder,代表一棵二元樹的前序遍歷(preorder traversal)和中序遍歷(inorder traversal)。請依據它們回傳此棵二元樹。
Example 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7]
Example 2:
Input: preorder = [-1], inorder = [-1] Output: [-1]
Solutions
前序、中序、後序遍歷為DFS的不同方法:
- 前序:
Root → Left → Right,我們得以確認根節點root(陣列首個元素) - 中序:
Left → Root → Right,在確認root值後,我們藉其拆分陣列成左右子樹
⭐Approach #1: Recursion
我們使用遞迴來實作:
- 從
preorder[0]得知root - 藉
root找到切出inorder中左右子樹的mid - 從
mid的左右節點出發,持續遞迴 - 當帶入的
preorder或inorder為空時,代表已構建到葉子節點
這樣的時間與空間複雜度皆為O(N)。
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
if not preorder or not inorder:
return None
root = TreeNode(preorder[0])
mid = inorder.index(preorder[0])
root.left = self.buildTree(preorder[1: mid + 1], inorder[:mid])
root.right = self.buildTree(preorder[mid + 1:], inorder[mid + 1:])
return root
# Test Case
## preorder = [3,9,20,15,7]
## inorder = [9,3,15,20,7]
😎108. Convert Sorted Array to Binary Search Tree
Description
給予一個升序整數陣列nums,請轉換成一高度平衡(height-balanced)的二元搜尋樹。
Example 1:

Input: nums = [-10,-3,0,5,9] Output: [0,-3,9,-10,null,5] Explanation: [0,-10,5,null,-3,null,9] is also accepted:

Example 2:

Input: nums = [1,3] Output: [3,1] Explanation: [1,null,3] and [3,1] are both height-balanced BSTs.
Solutions
Background Knowledge
- 中序(inorder)遍歷一個BST會得到一個升序陣列,但用陣列往回推則會得到多種BST
- 中序遍歷若配上一個後序(postorder)或前序(preorder)遍歷,則可導出唯一BST
- 題目要求此BST應為高度平衡(各節點的子樹高差應
<2)- 這代表選擇
root時皆得選擇範圍內的中間點 - 這在奇數數量的陣列沒有問題,但在偶數數量的陣列則因此會導出不同結果
- 這代表選擇
⭐Approach #1: Preorder Traversal (Choose Left Middle Node)
我們用前序遍歷(node -> left -> right)來建立高度平衡的BST:
- 定義函式
helper- 若邊界跨過彼此,代表已無節點做為子樹,回傳
None - 選取中間偏左的節點做為
root - 定好範圍,遞迴呼叫
helper,成為root的左右子樹 - 回傳
root
- 若邊界跨過彼此,代表已無節點做為子樹,回傳
- 呼叫
helper(0, len(nums) - 1),納入所有陣列元素
這樣的時間複雜度為O(N),空間複雜度為O(logN)。
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
def helper(left, right):
if left > right:
return None
p = (left + right) // 2
root = TreeNode(nums[p])
root.left = helper(left, p - 1)
root.right = helper(p + 1, right)
return root
return helper(0, len(nums) - 1)
😎110. Balanced Binary Tree
Description
給予一個二元樹,判斷其是否高度平衡(Height-Balanced, the depth of the two subtrees of every node never differs by more than one)。
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
Example 1:

Input: root = [3,9,20,null,null,15,7] Output: true
Example 2:

Input: root = [1,2,2,3,3,null,null,4,4] Output: false
Solutions
高度平衡是指任意節點的兩子樹深度差<2。我們會遍歷樹中所有節點,判斷是否有違反者,皆無就代表此樹為高度平衡。
Approach #1: Top-down recursion
我們由上往下地遞迴:
- 定義
height,判斷此節點的子樹高 - 定義
isBalanced,判斷此節點的左右子樹高差是否<2且其子節點亦若是
這樣的時間複雜度為O(NlogN)(節點呼叫height次數與樹高正相關),空間複雜度為O(N),N為節點數。
class Solution:
def height(self, root: TreeNode) -> int:
if not root:
return -1
return 1 + max(self.height(root.left), self.height(root.right))
def isBalanced(self, root: TreeNode) -> bool:
if not root:
return True
return abs(self.height(root.left) - self.height(root.right)) < 2 \
and self.isBalanced(root.left) \
and self.isBalanced(root.right)
⭐Approach #2: Bottom-up recursion
前述做法中,我們其實會重複計算各節點高度,若能避免則可提升效能。我們反著從底部往上判斷,回傳[是否平衡, 節點高度],就能利用已算好的結果。
這樣的時間與空間複雜度皆為O(N),N為節點數。
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def dfs(root):
if not root:
return [True, 0]
left, right = dfs(root.left), dfs(root.right)
balanced = left[0] and right[0] and abs(left[1] - right[1]) <= 1
return [balanced, 1 + max(left[1], right[1])]
return dfs(root)[0]
😎112. Path Sum
Description
給予一個二元樹根節點root和一個目標值targetSum,請判斷此樹從root到任一葉節點的值和能否等同targetSum。
Example 1:

Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 Output: true Explanation: The root-to-leaf path with the target sum is shown.
Example 2:
Input: root = [], targetSum = 0 Output: false Explanation: Since the tree is empty, there are no root-to-leaf paths.
Solutions
⭐Approach #1: Recursion
我們可用遞迴,在探索過程逐步減掉sum,並在碰到葉子時判斷sum是否為0。
這樣的時間為O(n),空間複雜度為O(logn),n為節點數。
class Solution:
def hasPathSum(self, root, sum):
if not root:
return False
sum -= root.val
# reach a leaf
if not root.left and not root.right:
return sum == 0
return self.hasPathSum(root.left, sum) or self.hasPathSum(root.right, sum)
😨124. Binary Tree Maximum Path Sum
Description
在二元樹的一個路徑(path),是指二元樹上任兩個節點(也可為同個節點)所連結起來的序列(包含此兩節點)。而路徑和(path sum),是指路徑中的節點值和。現在給予一個二元樹的根節點root,請回傳非空(non-empty)路徑中的最大路徑和。
Example 1:

Input: root = [1,2,3] Output: 6 Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
Example 2:

Input: root = [-10,9,20,null,null,15,7] Output: 42 Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
Solutions
難易度為困難的題目皆先跳過
😐137. Single Number II
Description
給予一個整數陣列nums,裡面元素僅一個出現一次,剩下的皆會出現三次。請找出此單數並回傳它。
Example 1:
Input: nums = [2,2,3,2] Output: 3
Example 2:
Input: nums = [0,1,0,1,0,1,99] Output: 99
Solutions
❌Approach #1: Sorting
若先排序再處理,答案就顯而易見。
這樣的時間複雜度為O(NlogN),空間複雜度為O(N)。
from typing import List
class Solution:
def singleNumber(self, nums: List[int]) -> int:
nums.sort()
for i in range(0, len(nums) - 1, 3):
if nums[i] == nums[i + 1]:
continue
else:
return nums[i]
return nums[len(nums) - 1]
❌Approach #2: Hash Map
若用雜湊表來記錄,答案也可輕鬆獲得
這樣的時間與空間複雜度皆為O(N)。
from typing import List
class Solution:
def singleNumber(self, nums: List[int]) -> int:
freq = {}
for num in nums:
if num not in freq:
freq[num] = 1
else:
freq[num] += 1
for key in freq:
if freq[key] == 1:
return key
⭐Approach #4: Equation for Bitmask
😎144. Binary Tree Preorder Traversal
Description
給予一棵二元樹節點root,請回傳此樹的前序(Preorder)遍歷。
Solutions
⭐Approach 1: Recursive Approach
前序遍歷的順序是優先讀取根節點、左子節點、右子節點,用遞迴實作一目了然。
這樣的時間與空間複雜度皆為O(N),N為節點數。
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
def helper(root):
if root:
res.append(root.val)
helper(root.left)
helper(root.right)
helper(root)
return res
😎145. Binary Tree Postorder Traversal
Description
給予一棵二元樹節點root,請回傳此樹的後序(Postorder)遍歷。
Solutions
⭐Approach 1: Recursive Approach
後序遍歷的順序是優先讀取左子節點、右子節點、根節點,用遞迴實作一目了然。
這樣的時間與空間複雜度皆為O(N),N為節點數。
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
def dfs(node):
if node:
dfs(node.left)
dfs(node.right)
res.append(node.val)
dfs(root)
return res
😐173. Binary Search Tree Iterator
Description
請實作一個疊代器(Iterator)來中序(In-order)遍歷一棵BST。它會具備:
BSTIterator(TreeNode root):初始化此類別- 根節點為類別成員之一
- 指標應被初始化為一個比BST內的值都小的數值
0 <= Node.val <= 106
boolean hasNext():判斷當前指標指向節點的右邊是否有節點int next():將指標移到右邊並回傳對應值
Example 1:

Input ["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"] [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []] Output [null, 3, 7, true, 9, true, 15, true, 20, false] Explanation BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]); bSTIterator.next(); // return 3 bSTIterator.next(); // return 7 bSTIterator.hasNext(); // return True bSTIterator.next(); // return 9 bSTIterator.hasNext(); // return True bSTIterator.next(); // return 15 bSTIterator.hasNext(); // return True bSTIterator.next(); // return 20 bSTIterator.hasNext(); // return False
Solutions
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
⭐Approach #1: Flattening the BST
我們先用一個陣列儲存中序(左子節點→根節點→右子節點)的遍歷結果。
這樣的時間複雜度,初始化耗時O(N),next()和hasNext()皆為O(1),空間複雜度為O(N)。
class BSTIterator:
def __init__(self, root: TreeNode):
self.sortedNodes = []
self.index = -1
self.inorder(root)
def inorder(self, root):
if not root:
return
self.inorder(root.left)
self.sortedNodes.append(root.val)
self.inorder(root.right)
def next(self) -> int:
self.index += 1
return self.sortedNodes[self.index]
def hasNext(self) -> bool:
return self.index + 1 < len(self.sortedNodes)
😐199. Binary Tree Right Side View
Description
給予一個二元樹根節點root,從上到下地遍歷樹中節點,但只回傳每層從右往左看的首個節點。
Example 1:

Input: root = [1,2,3,null,5,null,4] Output: [1,3,4]
Example 2:
Input: root = [1,null,3] Output: [1,3]
Example 3:
Input: root = [] Output: []
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
Solutions
⭐Approach #1: Iteration
此題與102. Binary Tree Level Order Traversal相似,皆需層層地遍歷節點,但僅保存從右往左看的首個節點。因為是層層遍歷,我們使用BFS的探索方式:
- 準備好
res和佇列q,將root加到q中 - 當
q內有節點時:- 遍歷每層節點,將
rightSide由左往右更新,故最後值為最右節點 - 當
rightSide為節點時,將其值加入res中()
- 遍歷每層節點,將
- 當
q內無節點時,res即為所求
這樣的時間複雜度為O(N),空間複雜度為O(D),N為節點數,D為直徑長。
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
res = []
q = collections.deque([root])
while q:
rightSide = None
for i in range(len(q)):
node = q.popleft()
if node:
rightSide = node
q.append(node.left)
q.append(node.right)
if rightSide:
res.append(rightSide.val)
return res
😎226. Invert Binary Tree
Description
給予一個二元樹的根節點(root),反轉此樹並再回傳根節點。
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
Example 1:

Input: root = [4,2,7,1,3,6,9] Output: [4,7,2,9,6,3,1]
Example 2:

Input: root = [2,1,3] Output: [2,3,1]
Solutions
⭐Approach #1: Recursive
我們持續遞迴呼叫invertTree:
- 當前節點為
None時,代表已遍歷完此支線的葉子節點,可以停止 - 繼續深入左右子節點
- 互換左右子節點
這樣的時間和空間複雜度皆為O(n),n為節點數。
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return None
right = self.invertTree(root.right)
left = self.invertTree(root.left)
root.left = right
root.right = left
return root
⭐Approach #2: Iterative
我們:
- 用個佇列
queue儲存每層節點 - 從
queue中拿出節點,互換左右子節點 - 若當前節點還有子節點,將它們放入
queue,等待下次迴圈的處理
這樣的時間和空間複雜度皆為O(n),n為節點數。
import collections
from typing import Optional
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return None
queue = collections.deque([root])
while queue:
current = queue.popleft()
current.left, current.right = current.right, current.left
if current.left:
queue.append(current.left)
if current.right:
queue.append(current.right)
return root
😐230. Kth Smallest Element in a BST
Description
給予一個BST的根節點root和一個整數k,請回傳樹中第k小的節點值。
Example 1:

Input: root = [3,1,4,null,2], k = 1 Output: 1
Example 2:

Input: root = [5,3,6,2,4,null,null,1], k = 3 Output: 3
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
Solutions
遍歷一棵樹可用兩種方法(DFS、BFS),而DFS又有三種策略(preorder、inorder、和postorder)。此處適合inorder,因為用inorder遍歷BST會得到一個升序陣列。
⭐Approach #1: Recursive Inorder Traversal
我們可以用遞迴法實作。
這樣的時間和空間複雜度皆為O(N),N為節點數。
class Solution:
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
def inorder(r):
if r:
# get ascending order of the tree
return inorder(r.left) + [r.val] + inorder(r.right)
else:
return []
return inorder(root)[k - 1]
⭐Approach #2: Iterative Inorder Traversal
我們可以用迭代法實作,搭配一個堆疊。
這樣的時間複雜度為O(H+k),空間複雜度為O(H),H為樹高。
class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
stack = []
curr = root
while stack or curr:
while curr:
stack.append(curr)
curr = curr.left
curr = stack.pop()
k -= 1
if k == 0:
return curr.val
curr = curr.right
😐235. Lowest Common Ancestor of a Binary Search Tree
Description
給予一個二元搜尋樹(BST),找出其中兩節點的最低共同祖先(lowest common ancestor,LCA)。
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
Example 1:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 Output: 6 Explanation: The LCA of nodes 2 and 8 is 6.
Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 Output: 2 Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
Solutions
此題與236. Lowest Common Ancestor of a Binary Tree可以互相參照。二元搜尋樹(BST)中的節點N會有以下特性:
- 左子樹節點值皆
≤N;右子樹節點皆>N - 左右子樹皆為BST
因此我們判斷BST兩節點的最低共同祖先,會:
- 從
root開始遍歷 - 若
p和q皆在當前節點的同邊(左或右),就可再往下判斷
⭐Approach #1: Recursion
我們將上述概念用遞迴實作:
p和q皆大於root(當下遍歷節點):往其右子節點判斷p和q皆小於root(當下遍歷節點):往其左子節點判斷- 以上皆非:當下遍歷節點即為所求
這樣的時間與空間複雜度皆為O(N)。
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if p.val > root.val and q.val > root.val:
self.lowestCommonAncestor(root.right, p, q)
elif p.val < root.val and q.val < root.val:
self.lowestCommonAncestor(root.left, p, q)
else:
return root
⭐Approach #2: Iteration
上述概念也可用疊代來實作。
這樣的時間複雜度為O(N),空間複雜度為O(1)。
class Solution:
def lowestCommonAncestor(self, root, p, q):
cur = root
while cur:
if p.val > cur.val and q.val > cur.val:
cur = cur.right
elif p.val < cur.val and q.val < cur.val:
cur = cur.left
else:
return cur
😨297. Serialize and Deserialize Binary Tree
Description
請設計一個演算法能夠以字串(String)為媒介,序列化(serialize)和反序列化(deserialize)二元樹(binary tree),設計方法沒有限制。
Example 1:

Input: root = [1,2,3,null,null,4,5] Output: [1,2,3,null,null,4,5]
Example 2:
Input: root = [] Output: []
Solutions
難易度為困難的題目皆先跳過
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Codec:
def serialize(self, root):
res = []
def dfs(node):
if not node:
res.append("N")
return
res.append(str(node.val))
dfs(node.left)
dfs(node.right)
dfs(root)
return ",".join(res)
def deserialize(self, data):
vals = data.split(",")
self.i = 0
def dfs():
if vals[self.i] == "N":
self.i += 1
return None
node = TreeNode(int(vals[self.i]))
self.i += 1
node.left = dfs()
node.right = dfs()
return node
return dfs()
😐450. Delete Node in a BST
Description
給予一個BST的根節點root和一個整數k,請回傳樹中第k小的節點值。
Example 1:
Input: root = [5,3,6,2,4,null,7], key = 3 Output: [5,4,6,2,null,null,7]

Solutions
⭐Approach #1: Recursion
知道BST的特性後,需額外處理的會是刪除對應節點後的處理:
- 遍歷節點,依據目標與節點值的大小深入其左子樹或右子樹
- 找到對應節點後,我們用其右子樹的最小節點來取代它
- 整體處理完後,樹即為所求
這樣的時間複雜度為O(logN),空間複雜度為O(H)。N為節點數,H為樹高。
class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
# Base case
if not root:
return root
# Go to the right subtree
if key > root.val:
root.right = self.deleteNode(root.right, key)
# Go to the left subtree
elif key < root.val:
root.left = self.deleteNode(root.left, key)
# Found the node
else:
# If the node has no children, just delete it
if not root.left:
return root.right
elif not root.right:
return root.left
# Find the min from right subtree, replace the node with it
cur = root.right
while cur.left:
cur = cur.left
root.val = cur.val
root.right = self.deleteNode(root.right, root.val)
return root
😎543. Diameter of Binary Tree
Description
給予一棵二元樹根節點root,請回傳此樹直徑(兩節點間最遠距離,不一定得包含root)。
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
Example 1:

Input: root = [1,2,3,4,5] Output: 3 Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].
Example 2:
Input: root = [1,2] Output: 1
Solutions
最遠距離必由兩葉子節點所構成,因為不然距離必可被其葉子節點延長。因為現在是二元樹,各節點連結僅會有其父節點和兩個左右子節點,所以實為求此樹中節點左右子樹和之最大值。
⭐Approach #1: Depth-first Search
我們:
- 用一個全域變數
res記錄最大長度 - 用DFS遍歷樹中節點:
- 算出其左右子樹高度和
- 與
res比較保留較大值
- 遍歷完樹後,
res即為所求
這樣的時間與空間複雜度皆為O(n)。
class Solution:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
res = 0
def dfs(root):
nonlocal res
if not root:
return 0
left = dfs(root.left)
right = dfs(root.right)
res = max(res, left + right)
return 1 + max(left, right)
dfs(root)
return res
😎572. Subtree of Another Tree
Description
給予兩個二元樹root和subRoot的根節點,判斷subRoot是否為root的子樹。
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
Example 1:

Input: root = [3,4,5,1,2], subRoot = [4,1,2] Output: true
Example 2:

Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] Output: false
Solutions
以下內容中,N為root節點數,M為subRoot節點數,情況成立時,N應≤M。
⭐Approach 1: Depth First Search
我們使用DFS來遍歷這兩棵樹:
- 定義
isSubtree:- 若已遍歷完
subRoot但仍沒回傳False,代表其為子樹 - 若已遍歷完
root但subRoot未遍歷完,那subRoot必不是子樹 - 用
sameTree判斷以此兩節點為根節點,是否為同樹
- 若不是,則改以其左右子節點為根節點,用
isSubtree判斷它們之一能否與子樹配
- 若已遍歷完
- 定義
sameTree:- 若兩節點皆為
None,那就是同樹 - 若兩節點值相同,則繼續判斷其子節點
- 以上條件皆未符合,代表它們為不同樹
- 若兩節點皆為
這樣的時間複雜度為O(M*N)(原樹每個節點得判斷M次),空間複雜度為O(M+N)。
class Solution:
def isSubtree(self, s: TreeNode, t: TreeNode) -> bool:
if not t:
return True
if not s:
return False
if self.sameTree(s, t):
return True
return self.isSubtree(s.left, t) or self.isSubtree(s.right, t)
def sameTree(self, s, t):
if not s and not t:
return True
if s and t and s.val == t.val:
return self.sameTree(s.left, t.left) and self.sameTree(s.right, t.right)
return False
Note:
在LeetCode官方詳解中還有另外兩個解法(String Matching、Tree Hash)。但因需要更多背景知識,面試時不一定能順利應用,在此不贅述。
😎606. Construct String from Binary Tree
Description
給予一個二元樹的根節點root,請用前序(preorder)遍歷樹,建構一個字串(整數和括號)。
Example 1:
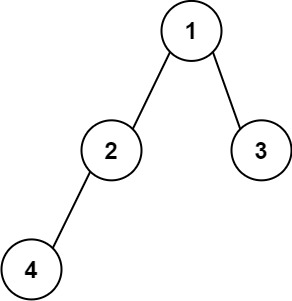
Input: root = [1,2,3,4] Output: "1(2(4))(3)" Explanation: Originally, it needs to be "1(2(4)())(3()())", but you need to omit all the unnecessary empty parenthesis pairs. And it will be "1(2(4))(3)"
Example 2:

Input: root = [1,2,3,null,4] Output: "1(2()(4))(3)" Explanation: Almost the same as the first example, except we cannot omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.
Solutions
Approach #1: Recursion
前序的遍歷順序為「中、左、右」,我們使用遞迴來處理:
這樣的時間與空間複雜度皆為O(N)。
class Solution:
def tree2str(self, node):
res = []
self.dfs(node, res)
return ''.join(res)
def dfs(self, node, res):
if not node:
return
res.append(str(node.val))
if not node.left and not node.right:
return
# 題目要求,即便左節點為空,只要右節點有值,仍要加上括號
res.append('(')
self.dfs(node.left, res)
res.append(')')
if node.right:
res.append('(')
self.dfs(node.right, res)
res.append(')')
😐701. Insert into a Binary Search Tree
Description
給予一個BST的根節點root和一數值v,請插入節點至BST後再回傳root。v保證不在原樹內,且解答可能不唯一。
Example 1:

Input: root = [4,2,7,1,3], val = 5 Output: [4,2,7,1,3,5]
Example 2:
Input: root = [40,20,60,10,30,50,70], val = 25 Output: [40,20,60,10,30,50,70,null,null,25]
Example 3:
Input: root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 Output: [4,2,7,1,3,5]
Solutions
⭐Approach #1: Recursion
將節點插入至BST的過程不需移動舊有節點,只需找到合適的空節點位置插入即可。
這樣的時間與空間複雜度皆為O(H),H為樹高。
class Solution:
def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
if not root:
return TreeNode(val)
if val > root.val:
root.right = self.insertIntoBST(root.right, val)
else:
root.left = self.insertIntoBST(root.left, val)
return root
⭐Approach #2: Iteration
我們也可以用疊代來處理。
這樣的時間複雜度為O(H),空間複雜度為O(1)。
class Solution:
def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
node = root
while node:
if val > node.val:
if not node.right:
node.right = TreeNode(val)
return root
else:
node = node.right
else:
if not node.left:
node.left = TreeNode(val)
return root
else:
node = node.left
return TreeNode(val)
😎783. Minimum Distance Between BST Nodes
Description
給予一個二元搜尋樹(BST)的根節點root,請回傳任兩節點的最小值差。
Example 1:

Input: root = [4,2,6,1,3] Output: 1
Example 2:

Input: root = [1,0,48,null,null,12,49] Output: 1
Solutions
⭐Approach #1: In-order Traversal with List
因為知道對BST的中序遍歷結果等同一個有序陣列,所以我們:
- 使用一個陣列儲存中序遍歷結果
- 遍歷陣列,找出兩兩鄰近元素差值的最小值
這樣的時間與空間複雜度皆為O(N)。
class Solution:
def __init__(self):
self.nodes = []
def inorderTraversal(self, root):
if not root:
return
# 中序順序:左子樹 -> 節點 -> 右子樹
self.inorderTraversal(root.left)
self.nodes.append(root.val)
self.inorderTraversal(root.right)
def minDiffInBST(self, root):
self.inorderTraversal(root)
res = float('inf')
for i in range(1, len(self.nodes)):
res = min(res, self.nodes[i] - self.nodes[i - 1])
return res
⭐Approach #2: In-order Traversal Without List
我們也可以在遍歷時就更新結果res,進而縮小空間複雜度。
這樣的時間複雜度為O(N),空間複雜度為O(H)。
class Solution:
def __init__(self):
self.res = float('inf')
self.prevValue = None
def inorderTraversal(self, root):
if not root:
return
self.inorderTraversal(root.left)
if self.prevValue:
self.res = min(self.res, root.val - self.prevValue.val)
self.prevValue = root
self.inorderTraversal(root.right)
def minDiffInBST(self, root):
self.inorderTraversal(root)
return self.res
😐1448. Count Good Nodes in Binary Tree
Description
給予一個二元樹根節點root,若某節點從root到其之間值最大,就是好(good)節點,請回傳樹中好節點數量。
Example 1:

Input: root = [3,1,4,3,null,1,5] Output: 4 Explanation: Nodes in blue are good. Root Node (3) is always a good node. Node 4 -> (3,4) is the maximum value in the path starting from the root. Node 5 -> (3,4,5) is the maximum value in the path Node 3 -> (3,1,3) is the maximum value in the path.
Example 2:

Input: root = [3,3,null,4,2] Output: 3 Explanation: Node 2 -> (3, 3, 2) is not good, because "3" is higher than it.
Example 3:
Input: root = [1] Output: 1 Explanation: Root is considered as good.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
Solutions
⭐Approach #1: Depth First Search, Recursion
此題適合用DFS來遍歷樹,它每次會把單條樹枝遍歷到底,再換另條繼續:
- 用
res統計好節點數量 - 當節點值
≥遍歷節點時,+1,並更新maxVal - 遍歷完所有節點後,
res即為所求
這樣的時間與空間複雜度皆為O(N)。
class Solution:
def goodNodes(self, root: TreeNode) -> int:
def dfs(node, maxValue):
if not node:
return 0
if node.val >= maxValue:
res = 1
maxValue = node.val
else:
res = 0
res += dfs(node.left, maxValue)
res += dfs(node.right, maxValue)
return res
return dfs(root, root.val)
😐1530. Number of Good Leaf Nodes Pairs
Description
給予一個二元樹根節點root,和整數distance。現在,樹中的葉節點對(Pair)會被稱為好(Good),如果彼此的最短距離≤ distance,distance介於1至10之間。
請回傳此樹中好葉節點對的數量。
Example 1:

Input: root = [1,2,3,null,4], distance = 3
Output: 1
Explanation: The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.
Example 2:

Input: root = [1,2,3,4,5,6,7], distance = 3
Output: 2
Explanation: The good pairs are [4,5] and [6,7] with shortest path = 2. The pair [4,6] is not good because the length of ther shortest path between them is 4.
Example 3:
Input: root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
Output: 1
Explanation: The only good pair is [2,5].
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
Solutions
Approach #1: Graph Conversion + BFS
我們關注找到葉子節點,這可用遍歷法(pre, in, post order)完成。但光靠原樹節點無法得到其父輩節點的索引,所以可轉化樹為無向圖(Undirected Graph),這樣圖中節點就皆有相連節點的索引。而要從未具權重的圖中找尋節點間的最短路徑,BFS相當適合。
- 用前序(pre-order)遍歷找出所有葉子節點,同時產出無向圖
- 用BFS,找出各葉子節點與其他葉子的最短距離,若
≤ distance則ans += 1
N為二元樹的節點數,這樣的時間複雜度為O(N2),空間複雜度為O(N)。
class Solution:
def _traverse_tree(self, curr, prev, graph, leaf_nodes):
if curr is None:
return
if curr.left is None and curr.right is None:
leaf_nodes.add(curr)
if prev is not None:
if prev not in graph:
graph[prev] = []
graph[prev].append(curr)
if curr not in graph:
graph[curr] = []
graph[curr].append(prev)
self._traverse_tree(curr.left, curr, graph, leaf_nodes)
self._traverse_tree(curr.right, curr, graph, leaf_nodes)
def countPairs(self, root, distance):
graph = {}
leaf_nodes = set()
self._traverse_tree(root, None, graph, leaf_nodes)
ans = 0
for leaf in leaf_nodes:
queue = []
seen = set()
queue.append(leaf)
seen.add(leaf)
for i in range(distance + 1):
# Clear all nodes in the queue (distance i away from leaf node)
# Add the nodes' neighbors (distance i+1 away from leaf node)
for j in range(len(queue)):
curr = queue.pop()
if curr in leaf_nodes and curr != leaf:
ans += 1
if curr in graph:
for neighbor in graph.get(curr):
if neighbor not in seen:
queue.append(neighbor)
seen.add(neighbor)
return ans // 2
⭐Approach #2: Post-Order Traversal
仔細想想,二元樹中兩節點的最短路徑必會通過其最低共同祖先(LCA),我們可藉此概念有效地算出葉節點間的最短距離。我們遍歷每個節點,視其為LCA並看其與子葉節點的距離和是否≤ distance,用遞迴彙整各節點為LCA時的滿足對數,最終結果即為所求。
- 定義輔助函式
post_order來遍歷各節點- 結果會回傳一個長為
12的陣列:[0]至[10]儲存與己相距對應距離的葉子節點數[11]儲存經此節點,為題目所求的葉子節點對數
- 遞迴呼叫此函式,從尾端葉節點開始統計,並讓
[11]累加
- 結果會回傳一個長為
- 呼叫輔助函式,其結果的
[11]即為所求
N為二元樹節點數,D為distance,H為樹高。這樣的時間複雜度為O(N * D2)≈O(N),空間複雜度為O(H)。
class Solution:
def _post_order(self, curr, distance):
if curr is None:
return [0] * 12
elif curr.left is None and curr.right is None:
curr = [0] * 12
curr[0] = 1
return curr
left = self._post_order(curr.left, distance)
right = self._post_order(curr.right, distance)
curr = [0] * 12
for i in range(10):
curr[i + 1] += left[i] + right[i]
curr[11] = left[11] + right[11]
for d1 in range(distance + 1):
for d2 in range(distance + 1):
if 2 + d1 + d2 <= distance:
curr[11] += left[d1] * right[d2]
return curr
def countPairs(self, root: TreeNode, distance: int) -> int:
return self._post_order(root, distance)[11]
